La force d'un mot de passe et comment la maximiser

23-12-2022

Temps de lecture estimé : 6 minutes

Dans l’illustration de l’article « À quoi joue la sécurisation d’un système d’information », quelque chose a dû vous surprendre : passé la deuxième colonne de classe de caractères, il est plus long de déchiffrer un mot de passe lorsqu’on descend d’un cran vers le bas plutôt que quand on avance d’un cran vers la droite. Autrement dit, il est plus sécurisant de rallonger notre mot de passe plutôt que de le rendre plus complexe. Mais alors pourquoi ? Cela voudrait-il dire que quand il s’agit de mot de passe, la taille ça compte ?

Pour comprendre comment fonctionne la force d’un mot de passe, commençons petit et prenons un cadenas à combinaison :

cadenas à combinaisons

Sur ce cadenas, 3 anneaux sont indépendants et les valeurs possibles sont les chiffres décimaux, le nombre de possibilités maximum est donc : 10 x 10 x 10 = 10^3 = 1000. Ces deux propriétés restent vraies pour un mot de passe quelconque, on peut alors exprimer nos possibilités comme dépendantes d’une base B, autrement dit le vocabulaire possible, et d’une longueur L : B^L.

Malheureusement, on se retrouve avec des valeurs sans unité, qui ne représentent qu’un nombre total de possibilités, là où on voudrait mesurer le « chaos » d’une information. Est-ce que le mot de passe 10 000 000 est aussi résistant aux attaques que Eiz1aik4 ?

Équivalence d’informations

On peut définir le chaos d’information comme la moyenne des répétitions parmi le total de possibilités. Là encore, commençons petit et imaginons une pièce lancée L fois. Dans cette situation binaire, le chaos serait de H = log2(2^L). Pour pouvoir comparer deux chaos informatiques, on applique exactement cette règle et on va donc tout rapporter à ça : c’est le log binaire de nos possibilités, soit H = log2(B^L). On appelle cette valeur l’entropie. Par facilité, on peut préférer la forme H = L x log2(B) qui met en lumière l’entropie d’un élément du vocabulaire.

On peut donc extraire un principe d’équivalence :

Un mot de passe de base B et de longueur L est aussi chaotique qu’une chaine de log2(B^L) bits choisie aléatoirement, quelle que soit la puissance des ordinateurs.

Ainsi, la force du mot de passe de notre cadenas correspond à une entropie d’environ 10 bits.

Une formule, deux variables

L’ANSSI préconise des mots de passe d’environ 80 bits, mais comment on y arrive ? Comme l’équation a plusieurs variables, il y a plusieurs moyens d’y parvenir. On pourrait par exemple obtenir 80 bits avec B = 13, L = 22 et B = 73, L = 13…

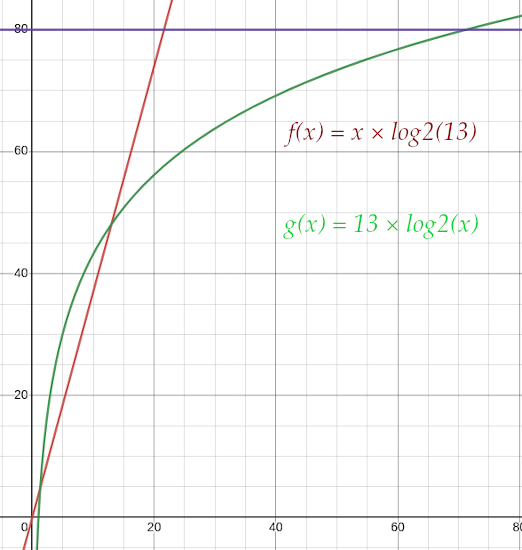
Courbe d’entropie de 80 bits

Ou alors avec B = 35, L = 16 et B = 5, L = 35.

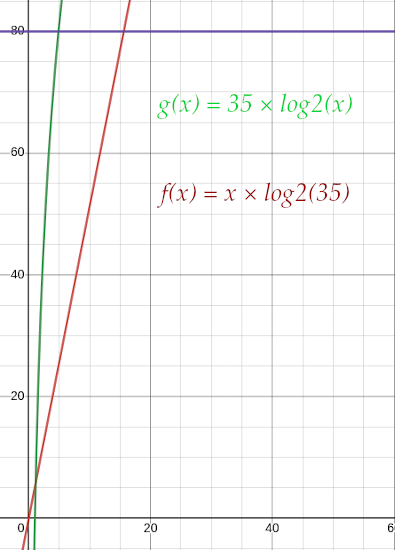
Courbe d’entropie de 80 bits

Mais quoi qu’il en soit, vous pouvez constater une chose notable : les courbes finissent toujours par se croiser, ce qui veut dire que l’avantage initial de B finit par s’écraser devant L. Et c’est bien normal : dans la forme H = L x log2(B), L croît de façon linéaire tandis que la croissance de B est logarithmique ! La différence des équations nous aide à le vérifier :

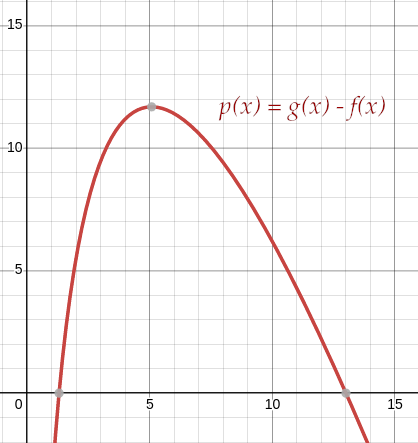
Entropie intersection

L’intersection présente ici à n = x = 13 reste vraie pour toute valeur. Ce que ça signifie est de première importance :

Tant que L < B, il est plus sécurisant d’augmenter la longueur L que de complexifier la base B.

Or, si l’augmentation du nombre de caractère est souvent unitaire, la complexification, elle, fonctionne par « saut » :

Classes de caractères	Entropie par caractère
Chiffre (10)	3,3
Hexadécimal (16)	4
Alphabétique sans casse (26)	4,7
Alphanumérique sans casse (36)	5,2
Alphanumérique avec casse (62)	6
ASCII imprimable (95)	6,5

De ce fait, L < B est vrai pour l’immense majorité des mots de passe, à plus forte raison en tenant compte des biais humains de construction.

/!\ NB: Bien qu’imparfaite, cette règle est une bonne approximation mentale. En réalité, il y a des effets de seuils et la “bascule” dépend de l’entropie par caractère.
Base \ Nombre de caractères 10 15 20 25 30 35 40 45 50 55 60
Chiffre 33 → 50 → 66 → 83 ↓ 100 ↓ 116 ↓ 133 ↓ 150 ↓ 166 ↓ 183 ↓ 199
Hexadécimal 40 → 60 → 80 → 100 → 120 ↓ 140 ↓ 160 ↓ 180 ↓ 200 ↓ 220 ↓ 240
Alphabétique sans casse 47 → 71 → 94 → 118 → 141 → 165 → 188 → 212 → 235 ↓ 259 ↓ 282
Alphanumérique sans casse 52 → 78 → 103 → 129 → 155 → 181 ↓ 207 ↓ 233 ↓ 259 ↓ 284 ↓ 310
Alphanumérique avec casse 60 → 89 → 119 → 149 → 179 → 208 → 238 → 268 → 298 ↓ 327 ↓ 357
ASCII imprimable 67 100 131 164 197 230 263 296 328 361 394

Base \ Nombre de caractères	10	15	20	25	30	35	40	45	50	55	60
Chiffre	33 →	50 →	66 →	83 ↓	100 ↓	116 ↓	133 ↓	150 ↓	166 ↓	183 ↓	199
Hexadécimal	40 →	60 →	80 →	100 →	120 ↓	140 ↓	160 ↓	180 ↓	200 ↓	220 ↓	240
Alphabétique sans casse	47 →	71 →	94 →	118 →	141 →	165 →	188 →	212 →	235 ↓	259 ↓	282
Alphanumérique sans casse	52 →	78 →	103 →	129 →	155 →	181 ↓	207 ↓	233 ↓	259 ↓	284 ↓	310
Alphanumérique avec casse	60 →	89 →	119 →	149 →	179 →	208 →	238 →	268 →	298 ↓	327 ↓	357
ASCII imprimable	67	100	131	164	197	230	263	296	328	361	394

Gagner du temps ?

Revenons un moment à la conclusion de l’article sur la sécurisation : si la sécurité, c’est du temps, alors il faut maximiser le temps pour se protéger. Or, si l’on parle depuis le début d’entropie, c’est parce qu’il y a un lien direct entre cette unité et la durée. À ce jour, il n’existe aucune méthode magique pour casser un mot de passe, il n’y a que deux méthodes principales : l’attaque par dictionnaire et l’attaque brute-force. Autrement dit… Il faut passer en revue des possibilités pour comparer la bonne valeur. En reprenant notre principe d’équivalence, on comprend que plus l’entropie sera élevée, plus il sera long pour un attaquant de trouver le bon.

Mais ce n’est pas suffisant. L’entropie est un excellent point de départ, mais j’ai évoqué plus haut l’attaque par dictionnaire. À entropie constante, si un dictionnaire contenait un texte populaire et ses variantes, serait-ce si long à casser ? Par exemple :

password
p4ssw0rd
P455w0rD

L’attaque par dictionnaire se base précisément sur ça, les variantes de mots de passe les plus populaires. Aussi, le meilleur moyen de maximiser sa protection c’est d’utiliser un mot de passe qui n’apparaît dans aucun dictionnaire possible. Et pour ça, rien de mieux que l’aléatoire, ce qui offre une autre vertu d’une sécurité maximale :

un mot de passe aléatoire offre la meilleure protection possible.

Mais fait amusant, utiliser un mot de passe quelque part créé de facto un dictionnaire où il existe, donc nous pouvons déduire un supplément :

pour protéger au maximum un mot de passe spécifique, il ne faut pas le réutiliser.

La génération et la mémorisation

Pour construire un bon mot de passe, reprenons les critères :

Si la longueur est inférieure à la base, le rallonger est plus sécurisant,
il doit être aléatoire (quitte à ce que ce soit par combinaison),
il doit être unique.

Mais en définitive, plusieurs forces sont à l’œuvre. Une force de construction qui pousse au renforcement et une autre plus terre à terre qui pousse à la simplicité : il faut bien se souvenir. Or, j’ai personnellement environ 240 mots de passe, impossible de respecter tous ces critères. Et si nous n’avions pas à nous en souvenir ?

Pour essayer par vous-même, vous avez cette fois deux options : vous pouvez étudier les courbes ou tenter de casser un mot de passe sur le dépôt d’exemple.

Sources :

Ce billet vous a plu ? Partagez-le sur les réseaux…

… Ou inscrivez-vous à la newsletter pour ne manquer aucun article (Si vous ne voyez pas le formulaire, désactivez temporairement uBlock).