Quand on programme, arrive un moment où une situation de répétition survient. Dans ce cas-là, se pose la question « récursion vs itération » : autrement dit, doit-on voir cette répétition comme une séquence à recommencer ou comme un problème constitué de lui-même ? C’est un choix très personnel, basé entre autres sur l’aisance du développeur avec la pratique et ce qu’il y projette (soyons honnêtes, nous sommes sujets à des biais).

De fait, la particularité de la récursivité, c’est son rapport à la combinaison. Prenons l’exemple de cette bonne vieille factorielle :

def factorialRecursive(n: Int): BigInt = {
  // Vérifiez toujours l'exhaustivité de la condition d'arrêt
  if (n < 0) {
    throw new IllegalArgumentException("n < 0")
  }
  if (n <= 1) {
    return 1
  }
  n * factorialRecursive(n-1)
}

def factorialIterative(n: Int): BigInt = {
  if (n < 0) {
    throw new IllegalArgumentException("n < 0")
  }
  var acc: BigInt = 1

  for (i <- 1 to n) {
    acc *= i
  }

  acc
}

Mathématiquement, fact(n) = n * fact(n-1), et cette définition par combinaison pousse à préférer un code la représentant directement. Ceci étant, on voit qu’il est parfaitement possible d’écrire un code itératif donc chacun peut trouver son compte.

Et si ce n’était pas seulement une histoire de préférence ? Et si, techniquement, il y avait une vraie différence entre les deux façons d’écrire ? Pour le comprendre, il est essentiel de se pencher sur le fonctionnement de la mémoire.

La pile et le tas

La pile (ou stack) et le tas (ou heap) sont deux formes de mémoire dans la RAM. Comme le nom peut le faire comprendre, la pile est plus organisée (donc plus accessible) mais avec l’inconvénient d’être beaucoup plus petite que le tas. Sous GNU/Linux sa taille est de 8192kio par thread (cf. ulimit -s), mais les langages peuvent en avoir une plus faible.

Elle est de plus un espace de stockage hyper volatile, dans le sens où elle se purge automatiquement quand le thread du processus se termine. Que stocke-t-elle ? Les fonctions, leurs arguments et leurs variables locales. Chaque nouvelle fonction empile une couche dans la mémoire, chaque fin de fonction l’enlève.

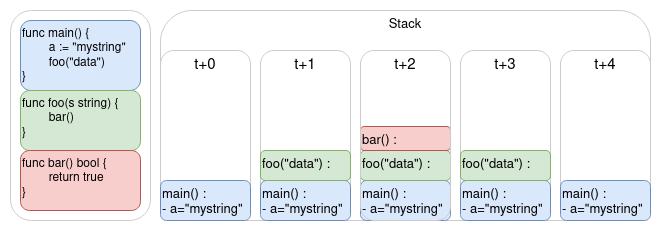
Revenons sur la distinction entre la récursion et l’itération. Puisque la récursion s’appelle elle-même, l’OS ajoute une frame pour chaque sous-appel de fonction. Et, 8Mio étant une taille finie, il existe un problème de taille suffisante pour que le programme crashe : c’est la fameuse stack overflow.

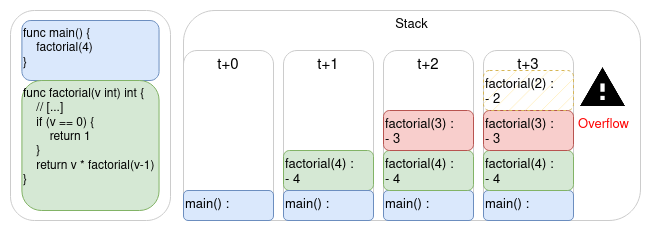
This is the end…

Est-il possible d’éviter ça ? Si la récursion est effectivement la forme syntaxique la plus adaptée au code, il existe une récursion dénommée la récursion terminale : elle est dite terminale si la récursion est la seule opération faite par le return. Pour cela, elle applique l’idée d’accumulateur de l’itération :

@tailrec
def factorialTailRecursive(n: Int, acc: BigInt): BigInt = {
  // Vérifiez toujours l'exhaustivité de la condition d'arrêt
  if (n < 0) {
    throw new IllegalArgumentException("n < 0")
  }
  if (n <= 1) {
    return acc
  }
  
  factorialTailRecursive(n-1, n*acc)
}

Avec ce format terminal, il n’est plus utile de stocker quoi que ce soit du contexte précédent la récursion, tout est porté par l’appel lui-même ; il n’y a donc pas d’accumulation sur la stack. Certains langages comme Scala ou OCaml suppriment d’ailleurs la frame de la stack : plus de stack overflow possible !

NB: Il faut bien comprendre le fonctionnement de votre langage avant d’appliquer la récursivité terminale et se faire surprendre par une stack overflow. Ni Go ni PHP ne fournissent d’optimisation par exemple. Une petite liste est présente en source.

Le problème évident de la récursion terminale

Si la récursivité terminale n’a que des avantages sur le papier, un schéma se dégage. La fonction « de niveau 1 » est appelable dans les mêmes conditions que la sous-fonction, c’est-à-dire avec les mêmes arguments, accumulateur compris. Il est donc possible de générer une incohérence :

def main(): Unit = {
  factorialTailRecursive(5, 12)
}

Le pire dans tout ça : la fonction n’a aucun moyen de se protéger vu qu’elle ne connaît pas son contexte d’exécution. Tout ce qu’on peut contrôler c’est :

• si acc < v, alors acc = 1,
• si acc > v, alors acc > v * (v+1).

Ce qui laisse beaucoup de possibilités d’erreurs.

Selon moi, cet inconvénient ne peut se résoudre que d’une façon : en embarquant la récursion dans une autre fonction, pour que la fonction de niveau 1 soit protégée d’un mésusage de son accumulateur. En reprenant notre exemple de la factorielle :

def factorialTailRecursive(n: Int): BigInt = {
  if (n < 0) {
    throw new IllegalArgumentException("n < 0")
  }
  @tailrec
  def inner(n: Int, acc: BigInt): BigInt = {
    if (n <= 1) {
      return acc
    }
    inner(n-1, n*acc)
  }

  inner(n, 1)
}

Personnellement, j’aime beaucoup la récursivité car elle apporte de la concision au sujet, et la récursivité terminale apporte de l’efficacité à l’élégance syntaxique. Mais cet avis personnel n’est vrai que parce que j’ai appris à penser « en mode récursif ». Quand le schéma apparaît, je me donne une règle de base : si je dois passer des heures à trouver le format pour écrire mon algo en récursif, c’est que je cherche à faire intelligent, pas lisible ou efficace. Donc je reste sur l’itératif.

Au bout du bout, la récursivité terminale embarquée est un filet de sécurité nécessaire si comme moi vous êtes à l’aise avec la récursion. Appliquer cette méthode, c’est rendre indescriptible un comportement interdit, donc c’est des bugs en moins.

Comme d’habitude, vous pouvez retrouver le code pour essayer par vous-même sur le dépôt d’exemple, y compris vérifier les consommations mémoires.

Sources:

• https://stackoverflow.com/questions/6171807/does-php-optimize-tail-recursion
• https://courses.cs.cornell.edu/cs3110/2021sp/textbook/data/tail_recursion.html
• https://en.wikipedia.org/wiki/Call_stack#Functions_of_the_call_stack
• https://en.wikipedia.org/wiki/Tail_call#Through_trampolining